Mag-lift
Joshua Cage
Chris Potters

​Magnetic Levitation
 
 
 
 
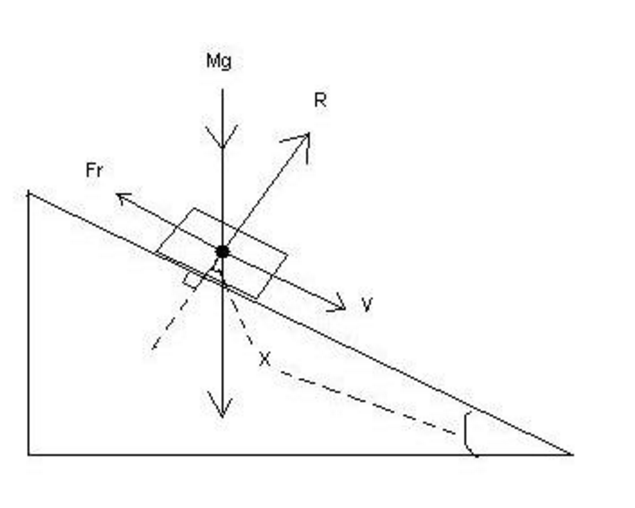
Mg = Mass X Gravity
V = Velocity
R = Reaction
Fr = Force of Resistance
μ = Coefficient of friction = Tan(θ)

Mg = R
Mg (Maglev) = 144g = R
Mg (Car) = 76g = R


For the first instance before the car moves, Mg = R
The force Mg and the Reaction (R) make an angle that is equal to angle θ (which defines the slope of the surface).
 
To calculate the force of R, we can use the Cos(θ). Since Cos = Adjacent / Hypotenuse, we plug in the numbers accordingly.
 
Mag Lev:
Cos(0.003266) = (R / 144)
 
(144)Cos(0.003266) = (R / 144) (144)������
 
(144)Cos(0.003266) = R
 
144 = R
 
Car:
Cos(3.67) = (R / 144)
 
(144)Cos(3.67) = (R / 144) (144)������
 
(144)Cos(3.67) = R
 
143.705 = R
​

Since we now know what the force of reaction is at angle θ, we can now use the formula:
 
Fr = μ * R
 
Since [R = Mg * Sin(θ)] , we can plug that in for R. And since [Fr = Mg * μ * Cos (θ)], we can set them equal to each other.
 
Mg * Sin(θ) = Mg * μ * Cos(θ)
 
Divide both sides by Mg.
 
Sin(θ) = μ * Cos(θ)
 
Divide by Cos(θ)
 
Sin(θ) / Cos(θ) = μ
 
μ = Tan(θ)
 
μ (Car) = Tan(3.67) = 0.06572
μ (Mag- Lev) = Tan(0.003266) = 0.000057
​

When car begins to move it means that Mg > R